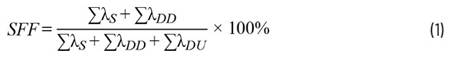摘 要:直扩系统的抗干扰能力由其处理增益决定,当其处理增益不足以对抗强干扰时,则需寻找其他干扰抑制来提高系统性能。本文研究了一种直扩信号的干扰抑制算法,对其工作原理进行了分析,给出了干扰复制和门限算法,并讨论了其中的非线性运算的dsp实现问题。
关键词:直接序列扩频;窄带干扰抑制;dsp;算法
algorithm and realization for narrow-band interference
suppression based on dsp in dsss communications
abstract:a direct sequence spread spectrum(dsss)system is well known for its inherent anti-jam character because of its processing gain.when the processing gain is not high enough to suppress the interference, some other effective methods must be found .this paper introduces an advanced way to suppress narrow band interference in dsss signal, analyzes its principle, and illuminates the dsp implementation of nonlinear algorithm.
keywords:direct sequence spread spectrum(dsss); narrow-band interference suppression; dsp; algorithm
直接序列扩频(dsss)通信系统具有很强的抗干扰能力,其抗干扰的能力与扩频增益是成正比的。但实际系统的频率资源总是有限的,当扩频增益受限,干扰的功率超过一定限度时,系统的性能将会下降,甚至造成通信中断,而其中窄带干扰最能严重破坏扩频通信性能[1]。为了提高直接序列扩频通信系统的窄带干扰抑制能力,使系统接收端获得较好的误码性能,借助于窄带干扰抑制技术来提高系统的性能用以弥补扩频增益的不足显得尤其重要。
一、窄带干扰抑制
干扰抑制技术通常分为两类:变换域滤波处理和时域的自适应滤波处理技术。时域的自适应滤波处理虽具有彻底的窄带干扰抑制能力,但当频率高时,调整滤波器系数以有效地去除干扰是非常困难的,这主要是因为一般的自适应滤波器,滤波器系数微小的改变,滤波器的输出就会发生很大的改变,而有时为了保证延时、相移、稳定性等,可能根本就无法实现。同时时域自适应滤波器收敛速度不快,比较适合于处理慢变的窄带干扰。
频域干扰抑制处理的一个最简化形式如图1所示。
这是一种成熟的广泛使用的窄带干扰抑制方法。但由于时域截断,会产生“截断”效应,实际应用中一般可采用加窗改善,但当处理的频率较高时,如70mhz中频,上述方法将很难得到满意的结果。
为了能克服以上两类方法的不足,利用可调谐数字外差滤波技术[2],它能够自适应精确跟踪干扰频率,并能控制陷波的带宽及深度,具有较高的灵活性和实用性。利用可调谐数字外差滤波器的接收机框图如图2所示。通过fft谱分析估计出干扰的频率后和干扰的宽度等参数后,由信号发生器单元产生出一个与干扰相同频率的信号,用此信号与接收到的信号r(k)相乘,即可将中频整个搬移到零频,此时采用一个滤波器即可以将干扰分离出来,再将滤波器输出信号搬移到最初频率位置,就得到了干扰信号的复制。其中滤波器的宽度由窄带干扰的宽度确定。这样,原信号与干扰的复制信号相减就可以有效抑制掉窄带干扰,而不会影响其它频率点的信号成分。采用图2的方法很容易对信号中的多个窄带干扰进行有效抑制。可以设计多路通道,每一路产生一个干扰信号的复制,将所有通道产生的干扰复制相加,就得到全部干扰信号的复制信号,再经过减法操作就把全部干扰都抑制掉了。这种方法的优点就是可以灵活控制干扰抑制过程中的陷波深度,同时,由于可以对fft的每一个数据进行处理,因此这种算法对干扰信号的变化具有很强的自适应能力。
这种方法的一个关键是跟踪干扰并确定干扰的频率,而确定干扰的频率的重要问题是干扰门限的确定。
二、窄带干扰门限算法
研究扩频信号(dsss信号加白色高斯噪声)的分布特性,在没有窄带干扰的情况下近似服从高斯分布。当加入窄带干扰后,信号的频谱分布发生了变化,窄带干扰对信号频谱分布的影响如图3所示。图3(a)表示没有窄带干扰情况下fft输出的幅度统计特性,图3(b)表示含有窄带干扰情况下的幅度统计特性,图中横坐标表示fft输出值的对数在没有干扰的情况下,可以求得每一块fft数据的统计特性。假设幅度的均值为μ,方差为σ2,则
<죐ģ녔ڳ춬甼ᒐͬ新ͬ>
从图中可以看到,绝大多数的信号分布在2σ范围内,如图3(a)所示。当加入一定数量的干扰信号或者增大干扰的能量后,如图3(b)所示,高斯分布的中心发生了偏移,由μ变到μi,标准差也由σ变到σi。同时由于窄带干扰相对于原信号而言有更大的能量,因此σi>σ。
取干扰抑制门限:
式中的m值是将求得的σ与4个预定的水平值σl0-σl3相比较