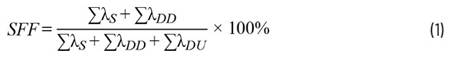一、引言
光纤传感由于具有本质安全、电绝缘性好、灵敏度高及便于连网等优点,已在许多物理量的测量中得到应用,特别是基于光纤干涉的传感系统已成为物理量检测中最为精确的系统之一。
光纤干涉仪是一种高精度测量仪器,但存在相位随机漂移及倍频等光学问题。现有文献报导中,解决的方法是采用相位生成载波技术,调制解调的实现过程复杂,并有可能产生信号波形的失真。另外,虽有采用压电陶瓷(pzt)的报导,但未见对相位随机漂移及倍频问题的具体解决方法。为此,本文给出一种简单实用的解决方案,在原理上说明其可行性,并进行了实验验证。
二、michelson干涉型光纤传感器原理
图1所示为michelson相位调制型光纤干涉仪结构示意图。由激光器发出的相干光经光隔离器和耦合器后一分为二分别送入2根长度基本相同的单模光纤(即干涉仪的两臂,其一为信号臂,另一参考臂),而后被反射膜反射,在耦合器的输出端发生干涉。显然,这是一种双光束干涉仪,干涉光的幅度与信号光及参考光的幅度有关,其相位为两臂光相位之差,干涉场光强分布为
i=i1+i2+2i1i2cos(φ)=a+bcos(φ)(1)
φ=2nπl/λ (2)
式(1)右端是光电转换的信号,i1、i2分别为干涉仪两臂单独存在时的光强,在检测时通常以直流项对待;2i1i2cos(φ)表示干涉效应,当φ=2mπ时,为干涉场的极大值,其中m为干涉级次。式(2)中,φ为干涉仪两臂光波的相位差,它可以表示为因为环境波动引起的随机漂移信号s和待测信号n之和,由光波波长λ、光纤折射率n以及光纤两臂长度差l共同决定。在波长一定的情况下,两臂光程差改变nl,就改变了干涉信号的相位差,从而实现传感功能。
图1 michelson光纤干涉仪的典型结构图干涉光信号由光电转换器(pd)转换为电信号。通过检测电信号的变化,就得到相应的干涉光信号的相位变化。
三、相位漂移及倍频原因简析
由式(1)可见,i随φ呈余弦变化规律,i~φ关系曲线如图2所示。在φ=2nπ处为最大值(n=0,±1,±2,……),而在φ=(2n+1π处取值最小,而在φ=nπ+π/2处变化最快,i变化最快即表示此时干涉仪具有最高灵敏度。
图2 双光束干涉的i~θ关系图所以,干涉仪应在工作在两臂光程差为π/2的位置,这样它的灵敏度最高;否则,当相位差在π或π的整数倍时,就几乎检测不到信号的变化。在实际探测过程中,即使事先调节两臂光程差为π/2,也会由于缓变的随机相位漂移噪声、偏振噪声及所处环境的某些无规则运动带来的噪声使静态时两臂光程差不能保持为π/2而出现相位漂移的现象,使输出发生漂移,如图3所示。
图3 随机相位漂移引起的零漂另外,由式(1)可知,在检测大信号时,若使两臂相位差改变量超过π/2就会出现倍频的现象,如图4所示。可见,此时输出信号不能反映实际信号。
图4 大信号引起的倍频现象四、采用pzt解决相位随机漂移及倍频问题
1. pzt的光纤相位调制原理
pzt具有压电效应。当电压加在pzt筒上时,pzt筒的外径周长会发生变化,从而使缠绕在pzt筒的光纤长度及折射率随之发生变化,改变光纤内传输的光波相位。
光纤相位变化量的数学表达式为
(3)式中,kl为光纤应变系数。由式(3)可知,相位调制的关键是分析光纤长度的变化量δl/l的规律。
图5 pzt筒结构如图5所示模型,pzt筒的高为h,电压u(t)加于内外半径r1、r2间。由于使用的pzt筒半径远大于厚度(即r2mr2-r1),所以在pzt筒内可以认为径向电场强度e为均匀分布。即
(4)式中,re=(r1+r2)/2为平均半径。根据弹性学理论构造柱面坐标系,可以把pzt筒看作是横向效应振子,即在径向施加电场,在圆周围方向发生应变。经过一系列公式推导,可以得到
(5)