电感式DC该如何设计?
电感是我们在变压器设计当中较长使用的一种元件,它的主要作用是把电能转化为磁能再存储起来。需要注意的是,虽然电感的结构类似于变压器,但是其只有一个绕组。本篇文章主要介绍了电感式DC-DC的升压器原理,并且本文属于基础性质,适合那些对电感的特性并不了解,但同时又对升压器感兴趣的朋友们。文中的一些原理性知识都能在网上查到,所以这里就不多家赘述了。
想要充分理解电感式升压原理,我们就必须首先知道电感的特性,包括电磁的转换与磁储能。这两点非常重要,因为我们所需要的所有参数都是由这两个特性引出来的。
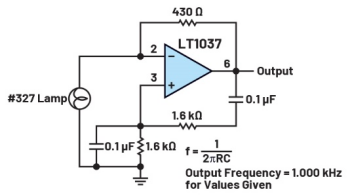
首先,我们先来观察下面的图:

各位朋友都知道,上图是电磁铁,一个电池对一个线圈通电。有人可能会奇怪,这么简单的图有什么好分析的呢?我们就是要用这张简单的图来分析它通电和断电的瞬间发生了什么。
线圈(以后叫作“电感”了)有一个特性---电磁转换,电可以变成磁,磁也可以变回电。当通电瞬间,电会变为磁并以磁的形式储存在电感内。而断电瞬磁会变成电,从电感中释放出来。
现在我们看看下图,断电瞬间发生了什么:

前面我说过了,电感内的磁能会在电感断电时重新变回电,然而问题来了:此时回路已经断开,电流无处可以,磁如何能转换成电流呢?很简单,电感两端会出现高压!电压有多高呢?无穷高,直到击穿任何阻挡电流前进的介质为止。
这里我们了解了电感的第二个特性----升压特性。当回路断开时,电感内的能量会以无穷高电压的形式变换回电,电压能升多高,仅取决于介质变的击穿电压。
现在我们对以上的内容作一下小结:
下面是正压发生器,你不停地扳动开关,从输入处可以得到无穷高的正电压。电压到底升到多高,取决于你在二极管的另一端接了什么东西让电流有处可去。如果什么也不接,电流就无处可去,于是电压会升到足够高,将开关击穿,能量以热的形式消耗掉。

然后是负压发生器,你不停地扳动开关,从输入处可以得到无穷高的负电压。

上面说的都是理论,现在来点实际的电子线路图,看看正/负压发生器的“最小系统”到底什么样子:
你可以很清楚看到演变,电路中仅仅把开关换成了三极管换而已。不要小看这两个图,事实上,所以开关电源都是由这两个图组合变换而来,所以掌握这两个图非常重要。

最后要提提磁饱合的问题。什么是磁饱合?
从上面的背景知道我们可以知道电感能储存能量,将能量以磁场方式保存,但能存多少呢?存满之后会发生什么情况呢?
1。存多少: “最大磁通量”这个参数就是干这个用的,很显然,电感不能无限保存能量,它存储能量的数量由电压与时间的乘积决定,对于每个电感来说,这是一个常数,根据这个常数你可以算出一个电感要提供N伏M安供电时必须工作于多高的频率下。
2。存满之后会如何: 这就是磁饱合的问题。饱合之后,电感失去一切电感应有的特性,变成一纯电阻,并以热的形式消耗掉能量。
经过分析和总结,相比大家都掌握了比较重要的几个核心电路图。并且也对其中的原理有了一定的理解,希望各位朋友能够充分理解这篇文章,从而灵活的应用到自己的设计当中去。
贴片电感的主要参数及其特性分析
我把一个223电容与一个电感串联,串联后再与一个223电容并联。然后量这个并联组件的电容,得出不可理解的值:多数这样的组件的电容是44-50nF之间,但有一些是一百多nF,有一些是几百nF(拆开后量,各个电容的值仍然是22nF)。

理论上的值应该是44nF,这些奇怪的电容值怎么理解呢?
讨论这个问题,用复数分析是最简捷最准确的。但这需要比较好的数学基础,能够从数学式中的各个量看出其物理意义。因此本帖尝试不用数学,仅用文字叙述。当然,这样只能进行定性的分析,不可能准确,同时比较冗长罗嗦,但可能物理意义比较清晰。分析如有错误或不当,还请版主及各位方家指正。
楼主提出的问题中有三个元件,稍复杂一些,我们先考虑两个元件,即一个电感和一个电容串联。
我们知道,串联电路中电流处处相同。这个相同,不仅是有效值相同,而且瞬时值也相同,也就是说,任何时刻都相同。我们又知道,电感和电容中电流与两端电压不同相,电容两端电压落后于电流90度,而电感两端电压超前于电流90度。现在电感和电容中电流相位相同,所以电感两端电压与电容两端电压相位相反,也就是说,任何时刻电容和电感上的电压是互相“抵消”的。

感抗和容抗都与频率有关。必定存在某一频率,在这个频率感抗与容抗相等。既然电感两端电压是感抗乘电流,电容两端电压是容抗乘电流,所以在这个频率下,电感两端电压恰与电容两端电压大小相等,方向相反,完全抵消。这就是串联谐振。
电感两端电压与电容两端电压完全抵消,那么电流不就是无穷大了?实际上电路中总有一些电阻,所以电流不会是无穷大,但电流很大是肯定的。此时串联电路呈纯阻性,即串联电路两端电压与电路中电流同相。
如果频率稍微降低一些怎么样?频率稍微降低一些,容抗变大一点,感抗变小一点,电容两端电压的大小稍微比电感两端电压的大小大一些,不能完全“抵消”,串联电路中电流仍比较大,注意比没有电感时要大,串联电路呈容性,当然不是纯容性,电路中还有一些电阻。从串联电路两端看,施加的电压没有变化,但电流比没有电感单纯是一个电容时大,好像是电容量变大了。可以这样考虑:感抗“抵消”了一部分容抗,使容抗减少,从串联电路两端看,就好像是电容量变大了。
应该注意到,现在容抗随频率的变化非常快,因为现在感抗与容抗互相“抵消”,频率变化一点点,“抵消”的程度就会差很多,也就是从串联电路两端看上去的电容量随频率很快变化,频率降低一点,“看上去”的电容量就会减少很多。
频率继续降低,感抗越来越小,容抗越来越大,直到感抗可以忽略,此时串联电路中电流与只存在一个电容时几乎相同,好像电感不存在。根据串联电路两端电压和其中的电流计算电容量,与没有电感几乎是相同的。频率非常低时,就可以认为是完全相同。
频率从谐振频率稍微升高一些,所有情况变得相反,现在电路呈感性,但感抗比没有电容时小,从串联电路两端看,好像是容抗“抵消”了一部分感抗,使电感量变小了。频率继续升高,容抗越来越小,感抗越来越大,直到容抗可以忽略,根据串联电路两端电压和其中的电流计算电感量,与没有电容时几乎相同。

对于电感和电容的并联电路,分析完全相同,只不过现在是并联,电感和电容两端电压相同,电感中电流和电容中电流相位相反,“抵消”的是电流而不是电压。
说句题外的话。《电路欣赏》版有一帖“振荡电路”,里面有位朋友提到皮尔斯振荡电路。皮尔斯振荡电路是晶体振荡器,晶体接在集电极与基极之间(皮尔斯当年实际是用电子管,那时还没有晶体管),集电极通过一个并联谐振回路接电源,发射极接地,基极除供给偏置电流的电路外并无其它。这个电路如何能振荡?实际上,我们知道晶体相当于一个很大的电感,集电极上的并联谐振回路稍有失谐,根据上面的分析,相当于一个电容。这样,集电极到基极是电感,集电极到发射极是电容,基极到发射极也是电容(分布电容),刚好构成三点电容式振荡电路(考毕兹电路),因此能够振荡。调节集电极上的并联谐振回路,可以改变这个等效的电容量,从而改变反馈量,控制振荡强度。所以这是个很方便使用的振荡电路。
根据上面的分析,还可以知道,测量电容或电感的结果,与测量时使用的频率有关。电路中总有分布电容和分布电感,这些分布电容和电感会影响测量结果,而且在离谐振频率比较近的地方,会造成很大的影响。因此测量电容或电感,应该使用与实际工作频率比较接近的频率去测量,这样比较能反映实际情况。
回到楼主的问题。一个22nF电容与电感串联,再与一个22nF电容并联,我们已经知道,22nF电容与电感串联后,可能相当于一个比22nF大的电容,也可能相当于一个电感,这与频率有关。一个比22nF大的电容与一个22nF电容再并联,当然是比44nF大的电容。至于几个不同的22nF电容测量结果相差很大,也容易理解。电容器都有误差,与电感串联后的谐振频率各不相同。我们也知道,测量使用的频率与谐振频率差一点,可能引起“看上去”的电容量很大的变化,因此各个不同的电容器这样与电感串联再与电容并联,测量的结果相差很大就是很正常的了。