With the widespread use of digital techniques in instrumentation and communications systems, a digitally-controlled method of generating multiple frequencies from a reference frequency source has evolved called Direct Digital Synthesis (DDS).
Fundamental DDS architecture
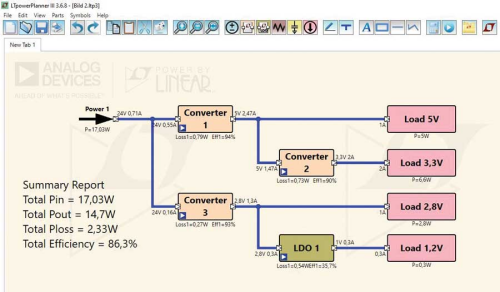
The basic architecture of Direct Digital Synthesis, shown in Figure 1 as a simplified model, shows a stable clock driving a programmable- read-only-memory (PROM), which stores one or more integral number of cycles of a sinewave (or other arbitrary waveform, for that matter). As the address counter steps through each memory location, the corresponding digital amplitude of the signal at each location drives a DAC, which in turn generates the analog output signal. The spectral purity of the final analog output signal is determined primarily by the DAC. The phase noise is basically that of the reference clock.

Figure 1: Fundamental direct digital synthesis system.
Because a DDS system is a sampled data system, all the issues involved in sampling must be considered: quantization noise, aliasing, filtering, etc. For instance, the higher order harmonics of the DAC output frequencies fold back into the Nyquist bandwidth, making them unfilterable, whereas, the higher order harmonics of the output of PLL-based synthesizers can be filtered. There are other considerations which will be discussed shortly.
A fundamental problem with this simple DDS system is that the final output frequency can be changed only by changing the reference clock frequency or by reprogramming the PROM, making it rather inflexible. A practical DDS system implements this basic function in a much more flexible and efficient manner using digital hardware called a Numerically Controlled Oscillator (NCO). A block diagram of such a system is shown in Figure 2.

Figure 2: A flexible DDS system.
The heart of the system is the phase accumulator, the contents of which are updated once each clock cycle. Each time the phase accumulator is updated, the digital number, M, stored in the delta phase register is added to the number in the phase accumulator register. Assume that the number in the delta phase register is 00...01 and that the initial contents of the phase accumulator are 00...00. The phase accumulator is updated by 00...01 on each clock cycle. If the accumulator is 32-bits wide, 232 clock cycles (over 4 billion) are required before the phase accumulator returns to 00...00, and the cycle repeats.
The truncated output of the phase accumulator serves as the address to a sine (or cosine) lookup table. Each address in the lookup table corresponds to a phase point on the sinewave from 0° to 360°. The lookup table contains the corresponding digital amplitude information for one complete cycle of a sinewave. (Actually, only data for 90° is required because the quadrature data is contained in the two MSBs). The lookup table therefore maps the phase information from the phase accumulator into a digital amplitude word, which in turn drives the DAC. This is shown graphically using the “phase wheel” in Figure 3.

Figure 3: Digital phase wheel.
Consider the case for n = 32, and M = 1. The phase accumulator steps through each of 232 possible outputs before it overflows and restarts. The corresponding output sinewave frequency is equal to the input clock frequency divided by 232. If M=2, then the phase accumulator register “rolls over” twice as fast, and the output frequency is doubled. This can be generalized as follows.
For an n-bit phase accumulator (n generally ranges from 24 to 32 in most DDS systems), there are 2n possible phase points. The digital word in the delta phase register, M, represents the amount the phase accumulator is incremented each clock cycle. If fc is the clock frequency, then the frequency of the output sinewave is equal to:
![]()
This equation is known as the DDS “tuning equation.” Note that the frequency resolution of the system is equal to fc/2n. For n = 32, the resolution is greater than one part in four billion. In a practical DDS system, all the bits out of the phase accumulator are not passed on to the lookup table, but are truncated, leaving only the first 13 to 15 MSBs. This reduces the size of the lookup table and does not affect the frequency resolution. The phase truncation adds a small but acceptable amount of phase noise to the final output. (See Figure 4).

Figure 4: Calculated output spectrum shows 90 dB SFDR for 15-bit phase truncation.
The resolution of the DAC is typically 2 to 4 bits less than the width of the lookup table. Even a perfect N-bit DAC will add quantization noise to the output. Figure 4 shows the calculated output spectrum for a 32-bit phase accumulator, 15-bit phase truncation. The value of M was chosen so that the output frequency was slightly offset from 0.25 times the clock frequency. Note that the spurs caused by the phase truncation and the finite DAC resolution are all at least 90 dB below the full-scale output. This performance far exceeds that of any commercially available 12-bit DAC and is adequate for most applications.
The basic DDS system described above is extremely flexible and has high resolution. The frequency can be changed instantaneously with no phase discontinuity by simply changing the contents of the M-register. However, practical DDS systems first require the execution of a serial, or byte-loading sequence to get the new frequency word into an internal buffer register which precedes the parallel-output M-register. This is done to minimize package pin count. After the new word is loaded into the buffer register, the parallel-output delta phase register is clocked, thereby changing all the bits simultaneously. The number of clock cycles required to load the delta-phase buffer register determines the maximum rate at which the output frequency can be changed.
Aliasing in DDS systems
There is one important limitation to the range of output frequencies that can be generated from the simple DDS system. The Nyquist Criteria states that the clock frequency (sample rate) must be at least twice the output frequency. Practical limitations restrict the actual highest output frequency to about 1/3 the clock frequency. Figure 5 shows the output of a DAC in a DDS system where the output frequency is 30 MHz and the clock frequency is 100 MHz. An anti-aliasing filter must follow the reconstruction DAC to remove the lower frequency (100 - 30 =70 MHz) as shown in the figure below.

Figure 5: Aliasing in a DDC system.
Note that the amplitude response of the DAC output (before filtering) follows a sin(x)/x response with zeros at the clock frequency and multiples thereof. The exact equation for the normalized output amplitude, A(f0), is given by:

where f0 is the output frequency and fc is the clock frequency.
This rolloff is because the DAC output is not a series of zero-width impulses (as in a perfect re-sampler), but a series of rectangular pulses whose width is equal to the reciprocal of the update rate. The amplitude of the sin(x)/x response is down 3.92 dB at the Nyquist frequency (1/2 the DAC update rate). In practice, the transfer function of the anti-aliasing filter can be designed to compensate for the sin(x)/x rolloff so that the overall frequency response is relatively flat up to the maximum output DAC frequency (generally 1/3 the update rate).
Another important consideration is that, unlike a PLL-based system, the higher order harmonics of the fundamental output frequency in a DDS system will fold back into the baseband because of aliasing. These harmonics cannot be removed by the anti-aliasing filter. For instance, if the clock frequency is 100 MHz, and the output frequency is 30 MHz, the second harmonic of the 30 MHz output signal appears at 60 MHz (out of band), but also at 100 – 60 = 40 MHz (the aliased component). Similarly, the third harmonic (90 MHz) appears inband at 100 – 90 = 10 MHz, and the fourth at 120 – 100 MHz = 20 MHz. Higher order harmonics also fall within the Nyquist bandwidth (dc to fc/2). The location of the first four harmonics are shown in Figure 5.
DDS systems as ADC clock drivers
DDS systems such as the AD9850 provide an excellent method of generating the sampling clock to the ADC, especially when the ADC sampling frequency must be under software control and locked to the system clock (see Figure 6). The true DAC output current IOUT, drives a 200 Ω, 42 MHz lowpass filter, which is source and load terminated, thereby making the equivalent load 100 Ω. The filter removes spurious frequency components above 42 MHz. The filtered output drives one input of the AD9850 internal comparator. The complementary DAC output current drives a 100 Ω load. The output of the 100 kΩ resistor divider placed between the two outputs is decoupled and generates the reference voltage for the internal comparator.

Figure 6: Using a DDS system as ADC clock drivers.
The comparator output has a 2 ns rise and fall time and generates a TTL/CMOS-compatible square wave. The jitter of the comparator output edges is less than 20 ps rms. True and complementary outputs are available, if required.
In the circuit shown (Figure 6), the total output rms jitter for a 40 MSPS ADC clock is 50 ps rms, and the resulting degradation in SNR must be considered in wide dynamic range applications.
Amplitude modulation in a DDS system
Amplitude modulation in a DDS system can be accomplished by placing a digital multiplier between the lookup table and the DAC input as shown in Figure 7. Another method to modulate the DAC output amplitude is to vary the reference voltage to the DAC. In the case of the AD9850, the bandwidth of the internal reference control amplifier is approximately 1 MHz. This method is useful for relatively small output amplitude changes as long as the output signal does not exceed the +1 V compliance specifications.

Figure 7: Amplitude modulation in a DDS system.
Spurious free dynamic range considerations in DDS systems
In many DDS applications, the spectral purity of the DAC output is of primary concern. Unfortunately, the measurement, prediction, and analysis of this performance is complicated by a number of interacting factors.
Even an ideal N-bit DAC will produce harmonics in a DDS system. The amplitude of these harmonics is highly dependent upon the ratio of the output frequency to the clock frequency. This is because the spectral content of the DAC quantization noise varies as this ratio varies, even though its theoretical rms value remains equal to q/√12 (where q is the weight of the LSB). The assumption that the quantization noise appears as white noise and is spread uniformly over the Nyquist bandwidth is simply not true in a DDS system (it is more apt to be a true assumption in an ADC-based system, because the ADC adds a certain amount of noise to the signal which tends to “dither” or randomize the quantization error. However, a certain amount of correlation still exists). For instance, if the DAC output frequency is set to an exact submultiple of the clock frequency, then the quantization noise will be concentrated at multiples of the output frequency, i.e., it is highly signal dependent. If the output frequency is slightly offset, however, the quantization noise will become more random, thereby giving an improvement in the effective SFDR.
This is illustrated in Figure 8 on the next page, where a 4096 (4k) point FFT is calculated based on digitally generated data from an ideal 12-bit DAC. In the left-hand diagram (A), the ratio between the clock frequency and the output frequency was chosen to be exactly 40, yielding an SFDR of about 77 dBc. In the right-hand diagram (b), the ratio was slightly offset, and the effective SFDR was increased to 94 dBc. In this ideal case, we observed a change in SFDR of 17 dB just by slightly changing the frequency ratio.

Figure 8: Effect of ratio of clock to output frequency on theoretical 12-bit DAC SFDR using 4096-point FFT.
Best SFDR can therefore be obtained by the careful selection of the clock and output frequencies. However, in some applications, this may not be possible. In ADC-based systems, adding a small amount of random noise to the input tends to randomize the quantization errors and reduce this effect.
The same thing can be done in a DDS system as shown in Figure 9 (See References 8, 9, 10). The pseudo-random digital noise generator output is added to the DDS sine amplitude word before being loaded into the DAC. The amplitude of the digital noise is set to about 1/2 LSB. This accomplishes the randomization process at the expense of a slight increase in the overall output noise floor. In most DDS applications, however, there is enough flexibility in selecting the various frequency ratios so that dithering is not required.

Figure 9: Injection of digital dither in a DDS system to randomize quantization noise and increase SFDR.
Analog Devices’ on-line design tool, ADIsimDDS, is an interactive tool to assist the user in selecting and evaluating DDS ICs. It allows the user to select a device, enter the desired operating conditions, and evaluate its general performance. The tool uses mathematical equations to approximate the overall performance of the selected devices and does not calculate all possible errors. Therefore, the tool should be used as a design aid only and is not intended to be used as a replacement for actual hardware testing and evaluation.
References
- Ask The Application Engineer—33: All About Direct Digital Synthesis (Analog Dialogue, Vol. 38, August 2004).
- “Single-Chip Direct Digital Synthesis vs. the Analog PLL,” (Analog Dialogue, Vol. 30, No. 3, 1996).
- “DDS Design”, By David Brandon, EDN, May 13, 2004.
- A Technical Tutorial on Digital Signal Synthesis, 1999, Analog Devices, Inc. Direct Digital Synthesis Frequently Asked Questions, Analog Devices, Inc.
- David Buchanan, “Choosing DACs for Direct Digital Synthesis,” Application Note AN-237, Analog Devices, Inc.
- David Brandon, “Direct Digital Synthesizers in Clocking Applications,” Application Note AN-823, Analog Devices, 2006.
- Richard J. Kerr and Lindsay A. Weaver, “Pseudorandom Dither for Frequency Synthesis Noise,” U.S. Patent 4,901,265, filed December 14, 1987, issued February 13, 1990.
- Henry T. Nicholas, III and Henry Samueli, “An Analysis of the Output Spectrum of Direct Digital Frequency Synthesizers in the Presence of Phase-Accumulator Truncation,” IEEE 41st Annual Frequency Control Symposium Digest of Papers, 1987, pp. 495-502, IEEE Publication No. CH2427-3/87/0000-495.
- Henry T. Nicholas, III and Henry Samueli, “The Optimization of Direct Digital Frequency Synthesizer Performance in the Presence of Finite Word Length Effects,” IEEE 42nd Annual Frequency Control Symposium Digest of Papers,” 1988, pp. 357-363, IEEE Publication No. CH2588- 2/88/0000-357.
- ADIsimDDS design tool from Analog Devices.
- Hank Zumbahlen, Basic Linear Design, Analog Devices, 2006, ISBN: 0-915550-28-1. Also available as Linear Circuit Design Handbook, Elsevier-Newnes, 2008, ISBN-10: 0750687037, ISBN-13: 978-0750687034. Chapter 4.
- Walt Kester, Analog-Digital Conversion, Analog Devices, 2004, ISBN 0-916550-27-3, Chapter 6. Also available as The Data Conversion Handbook, Elsevier/Newnes, 2005, ISBN 0-7506-7841-0, Chapter 6.