本文要讨论的这种设计可以将带通滤波器方案中的差分电路剔除在外,H.MarTInezetal.提供的方案属性则都有保留。
带通滤波器(BPF)被广泛用于通带非常窄、通带以外任何其它频率被衰减的应用。
公式(1)是带通滤波器的二阶带通传输函数:

其中K代表恒定的滤波器增益,Q代表滤波器的品质因数。
在H.MarTInezetal撰写的文章中,描述了一种具有可调品质因数、在谐振频率点具有恒定传输系数且采用三个运放设计的带通滤波器。这种滤波器的传输函数符合公式(1),其中K反比于品质因数Q。这种带可调品质因数的带通滤波器由一个双T单元和一个差分电路组成。
本文要讨论的这种设计可以将带通滤波器方案中的差分电路剔除在外,H.MarTInezetal.提供的方案属性则都有保留。
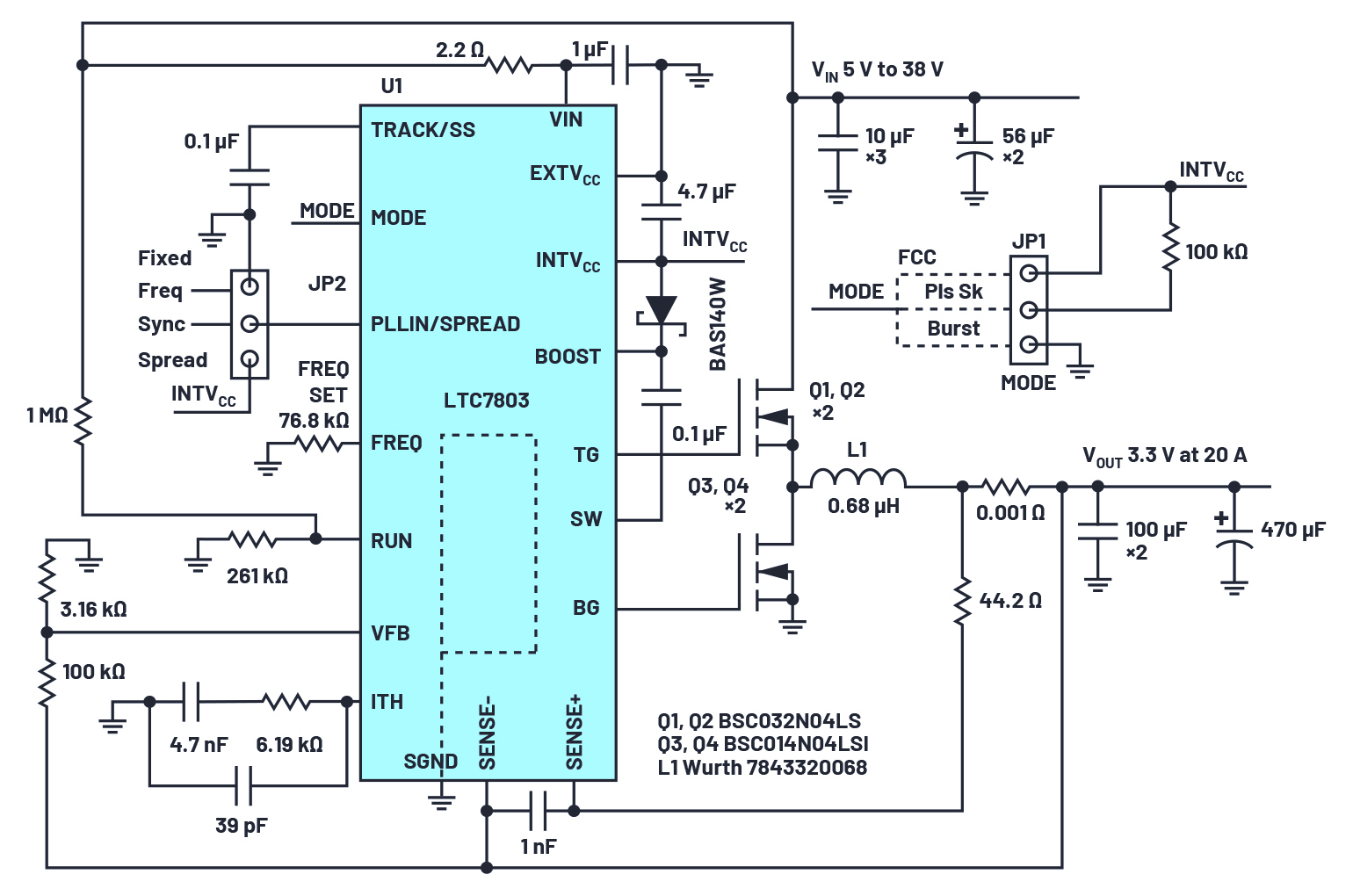
图1a所示的带通滤波器框图中有一个采用IC1和IC2的电压跟随器,它可以用一个标准的双运放并将其反相输入端连接到运放输出来实现。

图1:这种有源带通滤波器方案(a)可以改变品质因数,同时保持谐振频率点的增益系数不变。它基于的是没有差分放大器的双T单元(b)结构。
图1所示的带通滤波器基于的是一种双T型结构(图1b)。
根据(参考文献1中的公式2)设计的滤波器的增益函数公式是:

其中m是提供给双T单元(图1b)且与频率无关的正反馈系数。品质因数的值取决于电位器RPOT的位置。在电位器的底部位置,光标显示滤波器的品质因数Q处于最小值,当电位器向上调整时,品质因数随之增加。
正反馈系数m被定义为:

有源滤波器的谐振频率为:

公式2的品质因数Q为:

根据H.MarTInezetal.[1],当ω=ω0时最大增益AMAX总是保持不变,并等于1(0dB),与Q无关。m=0时品质因数最小,值为1/4,对应于电位器的转子连接到输入端。最大增益理论上是无穷大,但在实际应用中品质因数很难达到50以上。在典型应用中Q的变化范围从1到10。
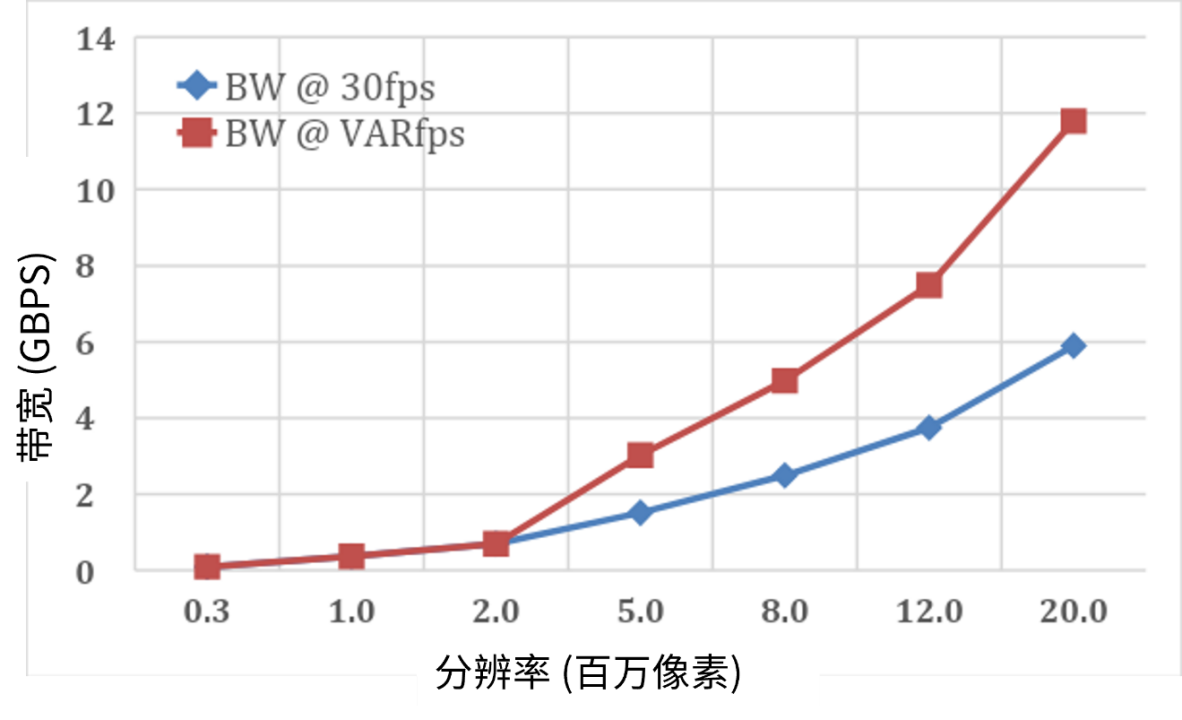
图2显示了带通滤波器输出VBP(s)/VIN(s)在m值从0.1到0.9变化时的波特图。从图中可以看出,频率f0等于1kHz。滤波器的建模是使用“SpectrumSoft”的(ECAD)Micro-CAP9电路仿真程序实现的。

图2:带通滤波器输出VOUT(t)的幅度和相位波特图。图中展示了将双T型单元的正反馈系数m从0.1变到0.9时产生的效果。
我们的方案是通过移动输入电压源Vin(t)的地线、将IC1和IC2组成的陷波滤波器的原始方案进行拓扑转换实现的。
这样,推荐电路就将附加的差分电路IC3(图3b)排除在外,达到了与Martinezetal相似的结果(图3a)。

图3:两种方案具有相同的传输函数。
(a)—Martinezetal.提供的方案;
(b)—我们的设计方案。
技术专区
- 慕尼黑电子展艾德克斯:结合配套软硬优势,提供最佳测试方案
- 益莱储与您相约EDICON 2018,助力客户踏上新征程
- 功率计数据测试不稳定该怎么办?
- 泰克解读物联网如何推动电源效率、测试策略的创新
- 基于TLC549数字电压表的设计